Diese Seite funktioniert nur mit Javascript.
Das klassische Ertragsgesetz3.2.3 Durchschnitts- und GrenzproduktSubstitutionale Produktionsfunktionen, Isoquanten
er Durchschnittsertrag ist eine der wichtigsten und verbreitetsten Kenngrößen in den Wirtschaftswissenschaften. Das ist nur deswegen nicht offensichtlich, da meist von spezifischen Durchschnittserträgen die Rede ist, z.B. der gesamtwirtschaftlichen Arbeitsproduktivität oder der Arbeitsstundenproduktivität. Die gesamtwirtschaftliche Arbeitsproduktivität ist das Bruttoinlandsprodukt pro Erwerbstätigen, die Arbeitsstundenproduktivität das Bruttoinlandsprodukt je geleisteter Arbeitsstunde (Arbeitsvolumen).
Durchschnittserträge lassen sich physisch und monetär und für alle oder Gruppen von Produktionsfaktoren definieren. Dabei wird immer ein Produktionsergebnis durch einen Faktoreinsatz geteilt. Z.B. beträgt das (physische) Durchschnittsprodukt der Arbeit in einer Stecknadelfabrik 40.000 Nadeln pro Tag und Arbeitskraft, wenn 10 Arbeitskräfte pro Tag 400.000 Nadeln produzieren. Kann eine Nadel zum Preis von 1 Cent verkauft werden, beträgt das bewertete Durchschnittsprodukt 400 Euro pro Tag und Arbeitskraft.
In der Folge bleiben Preise zunächst außen vor, d.h. es werden physische Durchschnittsproduktivitäten betrachtet. Die Begriffe Durchschnittsproduktivität, Durchschnittsprodukt und Durchschnittsertrag kann man übrigens weitestgehend synonym verwenden. Beim Begriff Durchschnittsertrag sollte man allerdings darauf achten, ihn nicht mit Durchschnittserlös oder Durchschnittsumsatz zu verwechseln. Lautet die Produktionsfunktion
$$ x = f(L) \tag{1} $$dann ist das Durchschnittsprodukt der Arbeit
$$ \text{DE} = \cfrac{x}{L} = \cfrac{f(L)}{L} \tag{1} $$wobei auf eine Indizierung von DE verzichtet wird, da mit $L$ nur ein Faktor betrachtet wird. Für das Zahlenbeispiel zum klassischen Ertragsgesetz gilt somit für den Durchschnittsertrag des Saatgutes
$$ x = -s^3 + 9s^2 +21s \tag{1a} $$ $$ \text{DE} = \cfrac{x}{s} = -s^2 + 9s +21 \tag{2a} $$wie schon aus dem vorigen Abschnitt bekannt ist. Der Durchschnittsertrag hängt hier vom Faktoreinsatz und damit von der Produktionshöhe ab. Wie das Automobilproduktions-Beispiel im vorigen Abschnitt gezeigt hat, muss das nicht so sein. Beim klassischen Ertragsgesetz ist es aber so.
Wenn man den Durchschnittsertrag grafisch ermitteln möchte, bietet es sich an, zwei Diagramme untereinander zu zeichnen (s. Abb. 1). Für die nun folgende Erklärung des Diagramms ist es wichtig zu wissen, wie man in einem Diagramm einen Durchschnittswert ablesen kann.
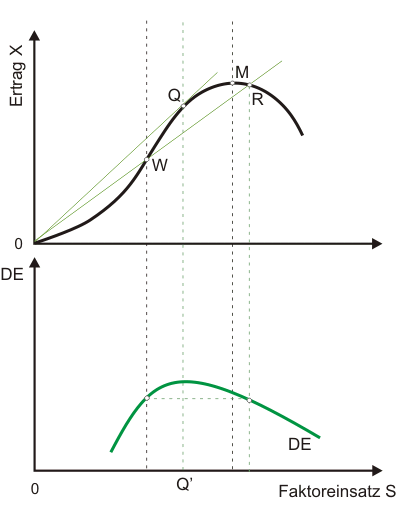
Das klassische Ertragsgesetz zeigt zwei markante Punkte, den Wendepunkt W und das Maximum M (im Wendepunkt verschwindet die zweite, im Maximum die erste Ableitung). Um den Durchschnittsertrag DE im unteren Diagramm abbilden zu können - nicht maßstabsgetreu, aber dem Verlauf nach - wird ein Ursprungsstrahl durch W gelegt, der die Ertragskurve ein weiteres Mal in R schneidet. Der durchschnittliche Ertrag muss somit in W und R übereinstimmen. Durch Linksdrehung dieses Strahls im Ursprung findet man den maximalen Durchschnittsertrag in Q, wo der Strahl die Ertragskurve tangiert. Kein anderer Strahl, der einen Punkt der Ertragskurve erreicht, besitzt einen steileren Anstieg. Da der Anstieg den Durchschnittsertrag anzeigt, ist dieser in Q maximal.
Wenn man sich nun vorstellt, einen Punkt vom Ursprung aus die Ertragskurve entlang wandern zu lassen, kann man erkennen, dass der Durchschnittsertrag bis Q ansteigt und anschließend abfällt. Für das Zahlenbeispiel sieht man dies mit der nach unten offenen Parabel aus Gleichung (2a) bestätigt. Augenscheinlich ist das Maximum des durchschnittlichen Ertrages bei einer anderen Faktoreinsatzmenge erreicht als das Maximum des Gesamtertrages.
Ein Konkurrenzanbieter (alle Preise sind fix) wird keinen Faktoreinsatz unter Q' wählen. Mit einem höheren Faktoreinsatz kann er den Gewinn auf jeden Fall steigern. Um das einzusehen, sei eine ungewöhnliche Größe betrachtet: der Gewinn pro Faktoreinheit. Wenn die Durchschnittsproduktivität bei einer Ausdehnung des Faktoreinsatzes ansteigt, dann muss der Gewinn ansteigen. Erstens wird pro Faktoreinheit mehr produziert, d.h. der Gewinn je Faktoreinheit steigt an, und zweitens werden mehr Faktoreinheiten eingesetzt. Konsequenz: Das Gewinnmaximum eines Anbieters bei vollkommener Konkurrenz kann nicht im Bereich steigender Durchschnittsproduktivitäten liegen.
In Abbildung 2 wird der (physische) Grenzertrag grafisch abgeleitet. Er zeigt (näherungsweise) an, um welchen Betrag die Produktion steigt, wenn der Faktoreinsatz um eine Einheit erhöht wird. Mathematisch entspricht der Grenzertrag der ersten Ableitung der Produktionsfunktion.
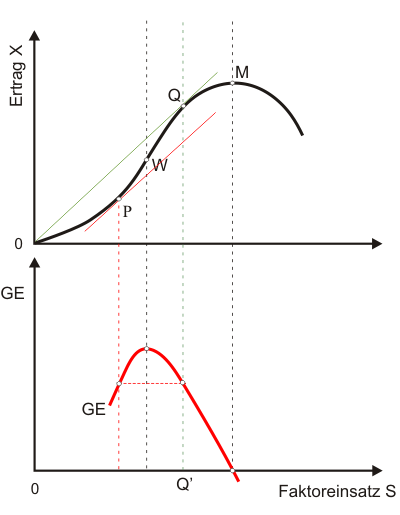
Auch für den Grenzertrag kann man synonym die Begriffe Grenzprodukt oder Grenzproduktivität verwenden. Sie ist als Kennzahl für die Produktivität in der wirtschaftspolitischen Diskussion weniger wichtig als die Durchschnittsproduktivität, aber in der Theorie kommt ihr die größere Bedeutung zu. So wird sich z.B. in der Folge noch zeigen, dass sich die Beschäftigung (und Entlohnung) eines Faktors nicht nach seiner Durchschnitts-, sondern nach seiner Grenzproduktivität richtet.
Mit der Methode des scharfen Hinsehens erkennt man den größten Grenzertrag im Punkt W (s. Abb. 2). Als weiterer Punkt wird der Punkt Q ausgewählt, der sich bei der Betrachtung des Durchschnittsertrages als interessant erwiesen hat. In Q ist eine Tangente angelegt (die durch den Ursprung verläuft - so wurde der Punkt ermittelt), die nach einer Parallelverschiebung die Ertragskurve auch in P tangiert. Der Grenzertrag stimmt somit in P und Q überein. Der Grenzertrag in M ist null und wird für größere Faktoreinsatzmengen negativ.
Allgemein lässt sich der Grenzertrag als erste Ableitung der Produktionsfunktion (1) angeben als
$$ \text{GE} = \cfrac{\text{d}x}{\text{d}L} = \cfrac{\text{d}f(L)}{\text{d}L} \tag{3} $$und für das Zahlenbeispiel ermittelt man
$$ \text{GE} = \cfrac{\text{d}x}{\text{d}s} = -3s^2 +18s +21 \tag{3a}$$Wie aus der Konstruktion von Grenz- und Durchschnittsertrag schon deutlich wurde, stimmen beide im Punkt Q überein. Wenn man die Abbildungen 1 und 2 zusammenführt, sieht man, dass der Grenzertrag den Durchschnittsertrag in dessen Maximum schneidet.
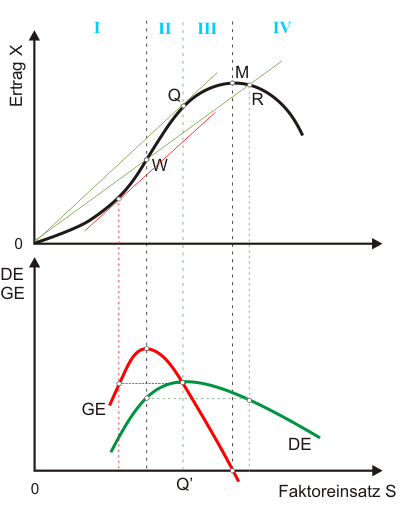
Bereich I: Durchschnitts- und Grenzerträge steigen
Bereich II: Grenzerträge sinken, Durchschnittserträge steigen
Bereich III: Grenz- und Durchschnittserträge sinken; neoklassischer Bereich; nur hier Gewinnmaximum eines Konkurrenzunternehmens möglich
Bereich IV: Grenzerträge negativ
In Gleichung (4) wird unter Ausnutzung der Quotientenregel der Durchschnittsertrag nach dem Faktoreinsatz differenziert und gleich null gesetzt. Die notwendige Bedingung für ein Maximum zeigt nach einfacher Umformung, dass Grenz- und Durchschnittsertrag übereinstimmen.
Für das Zahlenbeispiel ermittelt man
$$ \underbrace{-3s^2 +18s +21}_{\text{Grenzertrag}} = \underbrace{-s^2 + 9s +21}_{\text{Durchschnittsertrag}} \tag{4a} $$woraus man leicht berechnen kann, dass Grenz- und Durchschnittsertrag mit einem Wert von $x = 41,25$ bei $s = 4,5$ übereinstimmen.
Wenn man eine weitere Faktoreinheit einsetzt und die resultierende Produktionssteigerung größer als das aktuelle Durchschnittsprodukt ist, muss das Durchschnittsprodukt ansteigen: Wenn eine Person den Raum betritt, die größer ist als die Anwesenden im Schnitt, dann nimmt die Durchschnittsgröße zu. Das kann man auch kürzer ausdrücken: Wenn der Grenzertrag über dem Durchschnittsertrag liegt, steigt der Durchschnittsertrag an. Entsprechend gilt, wenn der Grenzertrag unter dem Durchschnittsertrag liegt, sinkt der Durchschnittsertrag. Konsequenz: Wenn der Grenzertrag gleich dem Durchschnittsertrag ist, ist der Durchschnittsertrag maximal.
Aus den Überlegungen zur Ermittlung von Elastizitäten ist bekannt, dass eine Gerade durch den Ursprung isoelastisch mit einem Wert von eins ist. Also besitzt das Klassische Ertragsgesetz in Q eine Elastizität von eins. In Q stimmen Durchschnitts- und Grenzproduktivität überein. Also zeigt eine Elastizität von 1 die Übereinstimmung von Durchschnitts- und Grenzproduktivität:
$$ E_{x,L} = \cfrac{\cfrac{\text{d}x}{x}}{\cfrac{\text{d}L}{L}} = \cfrac{\cfrac{\text{d}x}{\text{d}L}}{\cfrac{x}{L}} = \cfrac{\text{GE}}{\text{DE}} = 1 \space \Leftrightarrow \space \cfrac{\text{d}x}{\text{d}L} ={\cfrac{x}{L}} \tag{6} $$Diese Elastizität heißt partielle Produktionselastizität des Faktors Arbeit. Sie entspricht dem Verhältnis von Grenz- und Durchschnittsproduktivität. Aus der grafischen Darstellung erkennt man, dass die Produktion links von Q elastisch, rechts von Q unelastisch auf den Faktoreinsatz reagiert. Das vorangegangene Ergebnis, dass ein Anbieter bei vollkommener Konkurrenz bei steigenden Durchschnittserträgen nicht im Gewinnmaximum sein kann, lässt sich nun auch so formulieren: Wenn die partielle Produktionselastizität eines Faktors über eins liegt, kann kein Gewinnmaximum vorliegen. Eine analoge Aussage lässt sich auch für die gleichzeitige Variation aller Produktionsfaktoren ableiten (s.u. zum Begriff der Skalenelastizität).
Da es (hoffentlich) offensichtlich ist, dass kein gewinnmaximierender Anbieter im Bereich negativer Grenzerträge (IV in Abbildung 3) produzieren wird, kann ein Gewinnmaximum nur im dritten Bereich des Klassischen Ertragsgesetzes zu finden sein. Dieser Bereich, in dem die Grenzerträge positiv sind, abnehmen und unter den Durchschnittserträgen liegen, wird auch als neoklassischer Bereich bezeichnet. Gelten diese Eigenschaften für eine Produktionsfunktion durchgängig und nicht wie beim Klassischen Ertragsgesetz nur für einen Teilbereich, spricht man von einer neoklassischen Produktionsfunktion. Abbildung 4 zeigt eine solche Funktion, die man z. B. als $x = aL^b$ mit $a>0$ und $0 < b < 1$ spezifizieren kann.
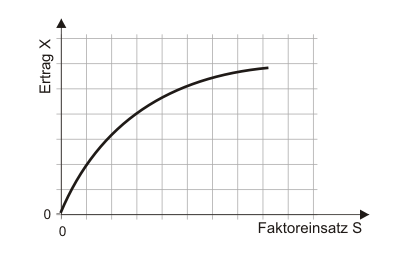
Da die Grenz- und Durchschnittserträge bei einer neoklassischen Produktionsfunktion von Beginn an abnehmen, liegen die Maxima von Grenz- und Durchschnittsertrag bei einem Faktoreinsatz von null (Randlösung).
Darunter versteht man das recht durchgängige empirische Phänomen, dass bei der Ausweitung des Faktoreinsatzes bei zahlreichen Produktionsprozessen zu beobachten ist, dass die Produktivität sinkt (das kann man so allgemein sagen, denn wenn die Grenzproduktivität sinkt, nimmt auch die Durchschnittsproduktivität ab). Formal gilt das Gesetz von der abnehmenden Grenzproduktivität, wenn die zweite (partielle) Ableitung der Produktionsfunktion negativ ist. Es ist das Pendant zum Gesetz vom abnehmenden Grenznutzen in der Haushaltstheorie.
Gesucht werden die vier Bereiche des Klassischen Ertragsgesetzes ($x$=Produktion, $L$=Faktoreinsatz):
$$ x = -L^3 + 16L^2 + 64L \tag{1} $$Berechnung des Durchschnittsertrages:
$$ \cfrac{x}{L} = -L^2 + 16L + 64 \tag{2} $$Ermittlung des Faktoreinsatzes, für den der Durchschnittsertrag maximal wird, durch Nullsetzen der ersten Ableitung
$$ \cfrac{\text{d(DE)}}{\text{d}L} = \cfrac{\text{d}\bigl(\cfrac{x}{L}\bigr)}{\text{d}L} = -2L +16 \overset{!}{=} 0 \space \Rightarrow \space L = 8\tag{3} $$Berechnung des Grenzertrages (erste Ableitung der Produktionsfunktion):
$$ \text{GE} = \cfrac{\text{d}x}{\text{d}L} = -3L^2 + 32L + 64 \tag{4} $$Überprüfung des Ergebnisses in (3), denn der Durchschnittsertrag ist maximal, wenn er gleich dem Grenzertrag ist:
$$ \underbrace{-3L^2 + 32L + 64}_{\text{Grenzertrag}} = \underbrace{-L^2 + 16L + 64 }_{\text{Durchschnittsertrag}} \space \Rightarrow \space L_1 = 0, L_2 = 8 \tag{5} $$Ermittlung des Faktoreinsatzes, für den der Grenzertrag maximal ist:
$$ \cfrac{\text{d}\bigl(\cfrac{\text{d}x}{\text{d}L}\bigr)}{\text{d}L} = -6L + 32 \overset{!}{=} 0 \space \Rightarrow \space L \approx 5,33\tag{6} $$Bestimmen des maximalen Ertrags durch Nullsetzen der Grenzertragsfunktion führt zu folgenden Lösungen
$$ L_{1,2} =\cfrac{32}{6} \pm \sqrt{\Bigl( \cfrac{32}{6} \Bigr)^2 + \cfrac{64}{3}} \tag{7} $$von denen der Wert $L_1 = 12,39$ ökonomisch interessant ist (der zweite Lösungwert ist $-1,72$ - der Faktoreinsatz kann aber nicht negativ sein.).
Damit ist festgestellt: Im Bereich I von $L=0$ bis $L=5,33$ nehmen die Grenzerträge zu. Im Bereich II von $L=5,33$ bis $L= 8,00$ nehmen die Grenzerträge ab und die Durchschnittserträge zu. Im Bereich III von $L= 8,00$ bis $L=12,39$ nehmen die Durchschnittserträge ab und sind die Grenzerträge positiv. Im Bereich IV mit $L \gt 12,39$ sind die Grenzerträge negativ.
Nach ähnlichen Seiten im WWW suchen